Из этого урока вы научитесь сравнивать рациональные числа.
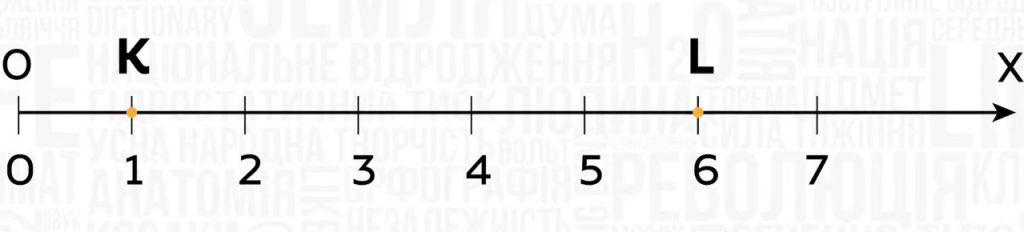 На координатном луче точка L с координатой 6 расположена правее точки К с координатой 1. Поэтому 6 > 1.
На координатном луче точка L с координатой 6 расположена правее точки К с координатой 1. Поэтому 6 > 1.
 На рисунке точка А с координатой три расположена правее точки В с координатой -6. Поэтому 3 > (-6).
Следовательно, большим из двух чисел есть число, расположенное на координатной прямой правее.
Помни, что на координатной прямой любое отрицательное число расположено левее любого положительного числа. Поэтому любое отрицательное число всегда меньше любого положительного числа.
На рисунке точка А с координатой три расположена правее точки В с координатой -6. Поэтому 3 > (-6).
Следовательно, большим из двух чисел есть число, расположенное на координатной прямой правее.
Помни, что на координатной прямой любое отрицательное число расположено левее любого положительного числа. Поэтому любое отрицательное число всегда меньше любого положительного числа.
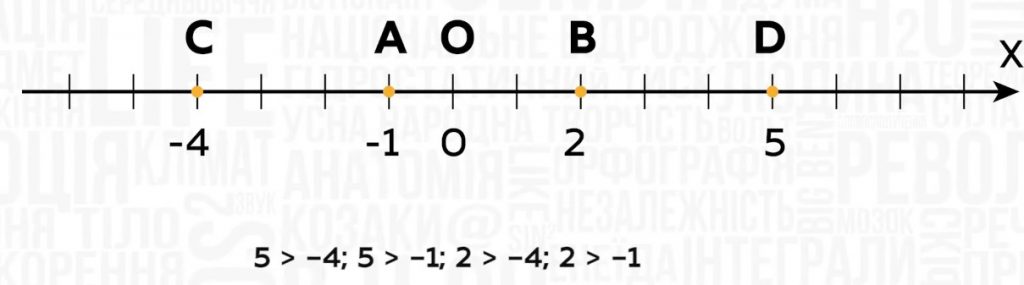 Например, пять больше минус четыре; пять больше минус один; два больше минус четыре; два больше минус один.
На рисунке точка А с координатой минус один лежит правее (ближе нуля) от точки С с координатой минус четыре, поэтому минус один больше минус четыре. Заметим, что модуль минус один меньше модуля минус четыре. Следовательно, из двух отрицательных чисел больше то, модуль которого меньше.
На координатной прямой число 0 расположено левее любого положительного числа и правее любого отрицательного числа.
Следовательно, любое положительное число больше нуля. Записывают в виде неравенства: a > 0.
Любое отрицательное число меньше нуля. Записывают в виде неравенства: a < 0.
Например, пять больше минус четыре; пять больше минус один; два больше минус четыре; два больше минус один.
На рисунке точка А с координатой минус один лежит правее (ближе нуля) от точки С с координатой минус четыре, поэтому минус один больше минус четыре. Заметим, что модуль минус один меньше модуля минус четыре. Следовательно, из двух отрицательных чисел больше то, модуль которого меньше.
На координатной прямой число 0 расположено левее любого положительного числа и правее любого отрицательного числа.
Следовательно, любое положительное число больше нуля. Записывают в виде неравенства: a > 0.
Любое отрицательное число меньше нуля. Записывают в виде неравенства: a < 0.
 модуль «а» равен «а», если «а больше или равен нулю»;
модуль «а» равен «-а», если «а меньше нуля».
модуль «а» равен «а», если «а больше или равен нулю»;
модуль «а» равен «-а», если «а меньше нуля».
 Какая из двух точек расположена справа от другой:
Какая из двух точек расположена справа от другой:

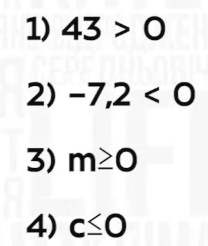 любое положительное число больше нуля, следовательно, 43 > 0;
любое отрицательное число меньше нуля, следовательно, -7,2 < 0;
поскольку «М» – не отрицательное число, то «М» ≥ 0;
поскольку «С» – не положительное число, то «С» ≤ 0.
любое положительное число больше нуля, следовательно, 43 > 0;
любое отрицательное число меньше нуля, следовательно, -7,2 < 0;
поскольку «М» – не отрицательное число, то «М» ≥ 0;
поскольку «С» – не положительное число, то «С» ≤ 0.
 На координатном луче точка L с координатой 6 расположена правее точки К с координатой 1. Поэтому 6 > 1.
На координатном луче точка L с координатой 6 расположена правее точки К с координатой 1. Поэтому 6 > 1.
 На рисунке точка А с координатой три расположена правее точки В с координатой -6. Поэтому 3 > (-6).
Следовательно, большим из двух чисел есть число, расположенное на координатной прямой правее.
Помни, что на координатной прямой любое отрицательное число расположено левее любого положительного числа. Поэтому любое отрицательное число всегда меньше любого положительного числа.
На рисунке точка А с координатой три расположена правее точки В с координатой -6. Поэтому 3 > (-6).
Следовательно, большим из двух чисел есть число, расположенное на координатной прямой правее.
Помни, что на координатной прямой любое отрицательное число расположено левее любого положительного числа. Поэтому любое отрицательное число всегда меньше любого положительного числа.
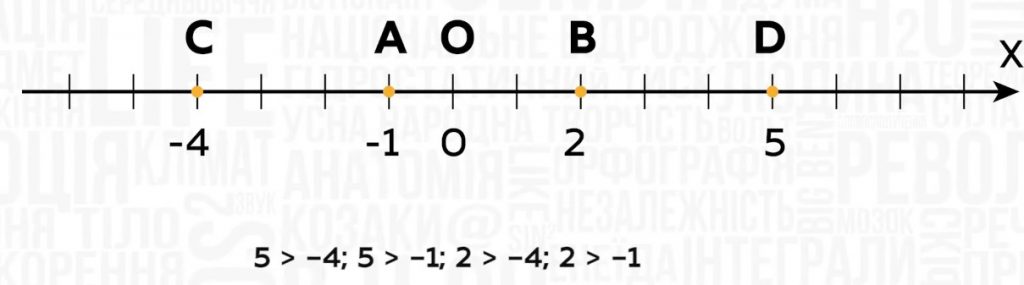 Например, пять больше минус четыре; пять больше минус один; два больше минус четыре; два больше минус один.
На рисунке точка А с координатой минус один лежит правее (ближе нуля) от точки С с координатой минус четыре, поэтому минус один больше минус четыре. Заметим, что модуль минус один меньше модуля минус четыре. Следовательно, из двух отрицательных чисел больше то, модуль которого меньше.
На координатной прямой число 0 расположено левее любого положительного числа и правее любого отрицательного числа.
Следовательно, любое положительное число больше нуля. Записывают в виде неравенства: a > 0.
Любое отрицательное число меньше нуля. Записывают в виде неравенства: a < 0.
Например, пять больше минус четыре; пять больше минус один; два больше минус четыре; два больше минус один.
На рисунке точка А с координатой минус один лежит правее (ближе нуля) от точки С с координатой минус четыре, поэтому минус один больше минус четыре. Заметим, что модуль минус один меньше модуля минус четыре. Следовательно, из двух отрицательных чисел больше то, модуль которого меньше.
На координатной прямой число 0 расположено левее любого положительного числа и правее любого отрицательного числа.
Следовательно, любое положительное число больше нуля. Записывают в виде неравенства: a > 0.
Любое отрицательное число меньше нуля. Записывают в виде неравенства: a < 0.
Модуль числа а
Если а – не отрицательное число (т.е. положительное или нуль), то пишут a ≥ 0. Читают: «а больше или равно нулю». Если а – не положительное число (т.е. отрицательное или ноль), то пишут а ≤ 0. Читают: «а меньше или равно нулю» Используя эти обозначения запишем свойство модуля числа а так: модуль «а» равен «а», если «а больше или равен нулю»;
модуль «а» равен «-а», если «а меньше нуля».
модуль «а» равен «а», если «а больше или равен нулю»;
модуль «а» равен «-а», если «а меньше нуля».
Решаем задачи
Задание 1:
 Какая из двух точек расположена справа от другой:
Какая из двух точек расположена справа от другой:
- N с координатой три целых пять десятых или С с координатой минус один;
- D с координатой минус два или О с координатой нуль;
- С с координатой минус один или D с координатой минус два;
- B с координатой b или С с координатой минус один;
- А с координатой а или В с координатой b.
Решение:

- точка N с координатой три целых пять десятых расположена справа от С с координатой минус один. Следовательно, три целых пять десятых больше минус один;
- точка О с координатой нуль расположена справа от D с координатой минус два. Следовательно, ноль больше минус два;
- точка С с координатой минус один расположена справа (ближе к нулю) от В с координатой В. Следовательно, минус один больше В;
- точка А с координатой а расположена справа от В с координатой b. Следовательно, «а» больше «b».
Задание 2:
Запишите в виде неравенства утверждение:- сорок три – положительное число;
- семь целых две десятых – отрицательное число;
- «М» – неотрицательное число;
- «С» – положительное число.
Решение:
 любое положительное число больше нуля, следовательно, 43 > 0;
любое отрицательное число меньше нуля, следовательно, -7,2 < 0;
поскольку «М» – не отрицательное число, то «М» ≥ 0;
поскольку «С» – не положительное число, то «С» ≤ 0.
любое положительное число больше нуля, следовательно, 43 > 0;
любое отрицательное число меньше нуля, следовательно, -7,2 < 0;
поскольку «М» – не отрицательное число, то «М» ≥ 0;
поскольку «С» – не положительное число, то «С» ≤ 0.
Задание 3:
Запишите числа -1,7; 0; -0,7; 0,2; 2; -2,85; 7,23; -2,84 в порядке убывания.Решение:
По условию следует записать числа от наибольшего к наименьшему. Наибольшим из чисел, расположенным на координатной прямой справа, является число 7,23. Затем 2; 0,2; 0. Поскольку среди отрицательных чисел наибольшее число то, у которого модуль наименьший, поэтому сравним модули отрицательных чисел:- |-0,7| = 0,7;
- |-1,7| = 1,7;
- |-2,84| = 2,84;
- |-2,85| = 2,85.
