Мішане число – це ціле число в поєднанні з дробом. Це комбінація цілого та дробового чисел. Наприклад, число 3 \frac{1}{2} це мішане число, де 3 – ціле число, а \frac{1}{2} – дробове.
Мішані числа використовуються для вираження величин, які більші за одиницю, але мають дробову частину. Вони широко використовуються в кулінарних рецептах, вимірюваннях та інших життєвих ситуаціях, де величини не завжди є цілими числами.
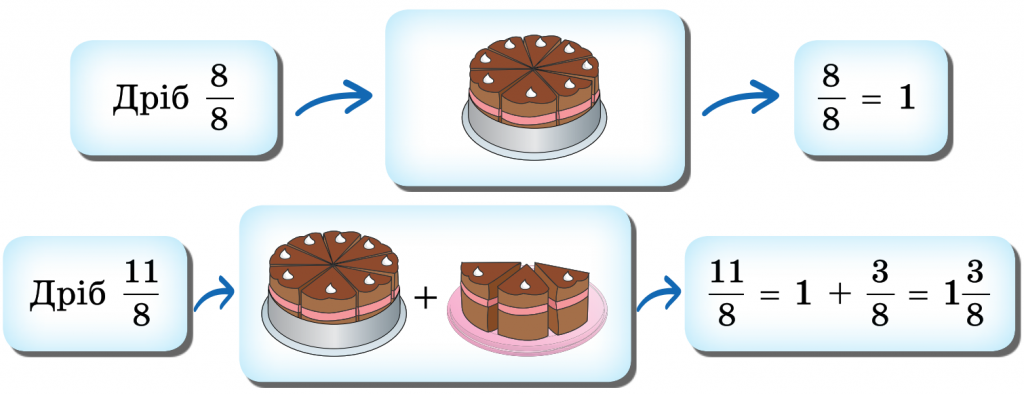
Щоб перетворити мішане число на неправильний дріб, ви можете просто помножити ціле число на знаменник і додати чисельник, а потім помістити цю суму над знаменником.
Наприклад:
2 \frac{3}{4} = (2 x 4) + 3 = 11 => \frac{11}{4} .
З іншого боку, щоб перетворити неправильний дріб на мішане число, потрібно розділити чисельник на знаменник і взяти частку як цілу частину мішаного дробу, а залишок – як чисельник дробової частини.
Наприклад:
\frac{11}{4} = 11 : 4 = 2 (ціла частина) і 11 – (2 ⋅ 4) = 3 (чисельник) => 2 \frac{3}{4}
Важливо зазначити, що мішані числа можна використовувати в математичних діях, таких як додавання, віднімання, множення і ділення, як і будь-які інші числа.
При роботі з мішаними числами слід пам’ятати, що їх може бути складніше порівнювати, ніж дроби без цілої частини. Порівнюючи мішані дроби, вам потрібно буде перетворити їх у неправильні дроби зі спільним знаменником, перш ніж робити порівняння.
Існують також інші форми представлення мішаних чисел, наприклад, ви можете представити мішане число у вигляді десяткового дробу, що є способом вираження числа у вигляді комбінації цілих чисел і десяткових дробів.
Отже, мішані числа є важливим інструментом для вираження та роботи з величинами, які не завжди є цілими числами. Їх можна використовувати в математичних операціях і вимірюваннях, а також перетворювати в інші форми представлення залежно від контексту або завдання.
Звичайні дроби 5 клас
