Самостійна робота Лінійна функція, її графік і властивості 7 клас Алгебра

Самостійна робота призначена для учнів 7 класу за програмою НУШ на тему “Лінійна функція, її графік і властивості”. Пропонується розв’язати 6 завдань різного рівня складності та 4 варіанти. Ця самостійна робота допоможе учням та вчителю перевірити знання теми. Автор М. Якир – від Мерзляків

Варіант 1

1. Яка з даних функцій не є лінійною?

y = 4x + 7

y = \frac{2x}{7}

y = x

y = \frac{5}{x}

2. Укажіть координати точки перетину графіків функцій $y = 3x + 6$ і $y = 30 - 5x$ .

1) (3; 15)

2) (15; 3)

3) (18; 60)

4) (60; 18)

3. Функцію задано формулою $y = 7x - 6$ . Знайдіть:
1) значення функції, якщо значення аргументу дорівнює -3;
2) значення аргументу, при якому значення функції дорівнює 22.

4. Побудуйте графік функції $y = 1,5x + 6$ . Користуючись графіком, знайдіть значення аргументу, при яких функція набуває додатних значень.

5. Задайте формулою функцію, графік якої зображено рисунку.

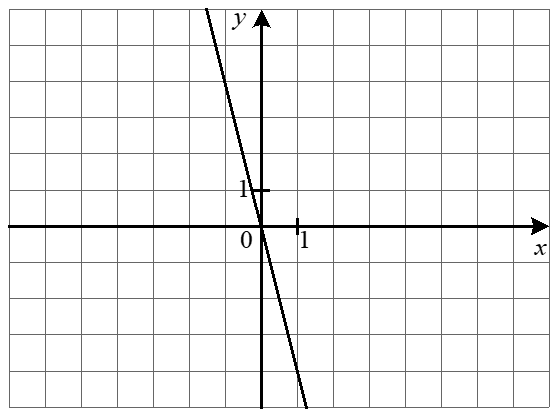
6. Побудуйте графік функції $f(x) = \begin{cases} x + 5, & \text{якщо } x < -2, \\ 1 - x, & \text{якщо } -2 \leq x \leq 3, \\ 2x - 8, & \text{якщо } x > 3. \end{cases}$ і визначте, при яких значеннях $m$ графік функції $y = m$ має з графіком функції $f$ рівно дві спільні точки.

Варіант 2

1. Яка з даних функцій не є лінійною?

y = 8x - 5

y = -x

y = \frac{x}{3}

y = \frac{8}{x}

2. Укажіть координати точки перетину графіків функцій $y = 4x - 9$ і $y = 27 - 2x$ .

1) (6; 15)

2) (15; 6)

3) (9; 27)

4) (9; 11)

3. Функцію задано формулою $y = 11x - 2$ . Знайдіть:
1) значення функції, якщо значення аргументу дорівнює -4;
2) значення аргументу, при якому значення функції дорівнює 31.

4. Побудуйте графік функції $y = 2,5x - 5$ . Користуючись графіком, знайдіть значення аргументу, при яких функція набуває від’ємних значень.

5. Задайте формулою функцію, графік якої зображено рисунку.

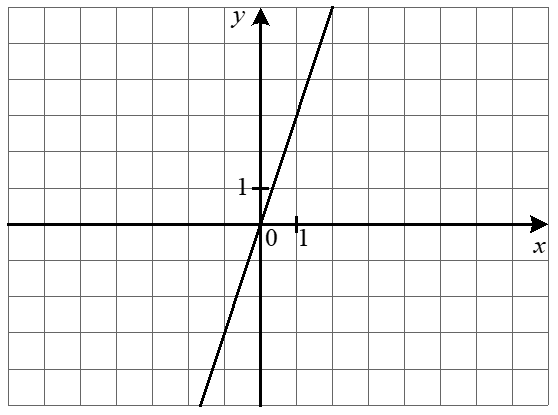
6. Побудуйте графік функції $f(x) = \begin{cases} 3x + 15, & \text{якщо } x < -4, \\-x - 1, & \text{якщо } -4 \leq x \leq 1, \\x - 3, & \text{якщо } x > 1.\end{cases}$ і визначте, при яких значеннях $m$ графік функції $y = m$ має з графіком функції $f$ рівно дві спільні точки.

Варіант 3

1. Яка з даних функцій не є лінійною?

y = \frac{x}{x}

y = 4x - 1

y = 6

y = -\frac{x}{2}

2. Укажіть координати точки перетину графіків функцій $y = 0,2x + 9$ і $y = 3 - 0,3x$ .

1) (12; 11,9)

2) (-12; 6,6)

3) (1,2; 11,4)

4) (-120; -15)

3. Функцію задано формулою $y = \frac{x}{3} - 3$ . Знайдіть:
1) значення функції, якщо значення аргументу дорівнює -9;
2) значення аргументу, при якому значення функції дорівнює 7.

4. Побудуйте графік функції $y = -3x + 12$ . Користуючись графіком, знайдіть значення аргументу, при яких функція набуває додатних значень.

5. Задайте формулою функцію, графік якої зображено рисунку.

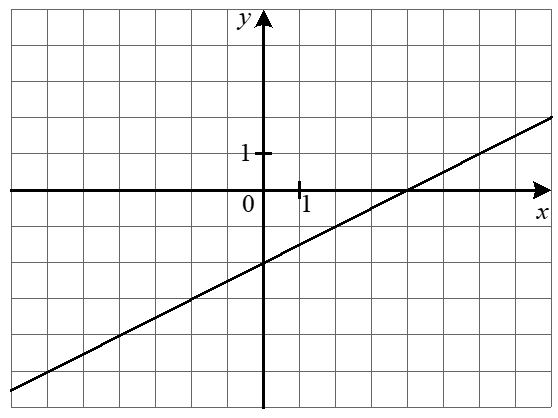
6. Побудуйте графік функції $f(x) = \begin{cases} 2.5x - 2, & \text{якщо } x < 2, \\-2.5x + 8, & \text{якщо } 2 \leq x \leq 4, \\x - 6, & \text{якщо } x > 4.\end{cases}$ і визначте, при яких значеннях $m$ графік функції $y = m$ має з графіком функції $f$ рівно дві спільні точки.

Варіант 4

1. Яка з даних функцій не є лінійною?

y = 0,8x

y = 5x - 3

y = -5

y = 3x^2

2. Укажіть координати точки перетину графіків функцій $y = 0,1x + 1$ і $y = 9 - 0,3x$ .

1) (20; 3)

2) (40; 5)

3) (2; 1,2)

4) (20; 21)

3. Функцію задано формулою $y = -\frac{x}{2} + 3$ . Знайдіть:
1) значення функції, якщо значення аргументу дорівнює -14;
2) значення аргументу, при якому значення функції дорівнює 6.

4. Побудуйте графік функції $y = 0,6x + 3$ . Користуючись графіком, знайдіть значення аргументу, при яких функція набуває від’ємних значень.

5. Задайте формулою функцію, графік якої зображено рисунку.

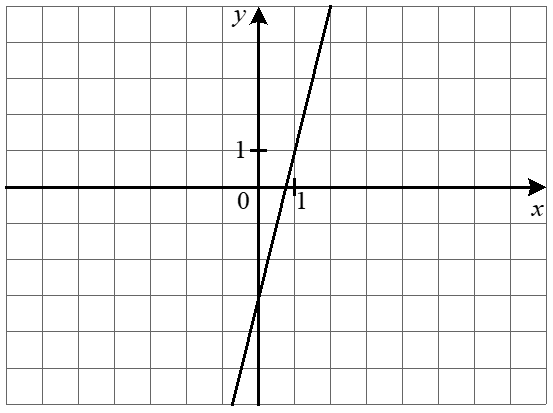
6. Побудуйте графік функції $f(x) = \begin{cases} 3x + 2, & \text{якщо } x < -1, \\ -3x - 4, & \text{якщо } -1 \leq x \leq 1, \\ 2x - 9, & \text{якщо } x > 1. \end{cases}$ і визначте, при яких значеннях $m$ графік функції $y = m$ має з графіком функції $f$ рівно дві спільні точки.

Завантажити Самостійну роботу Лінійна функція, її графік і властивості для друку