Смешанное число — это целое число в сочетании с дробью. Это комбинация целого и дробного чисел. Например, число 3 \frac{1}{2} это смешанное число, где 3 — целая часть, а \frac{1}{2} — дробная.
Смешанные числа используются для выражения величин, которые больше единицы, но имеют еще дробную часть. Они широко используются в кулинарных рецептах, измерениях и других жизненных ситуациях, где величины не всегда являются целыми числами.
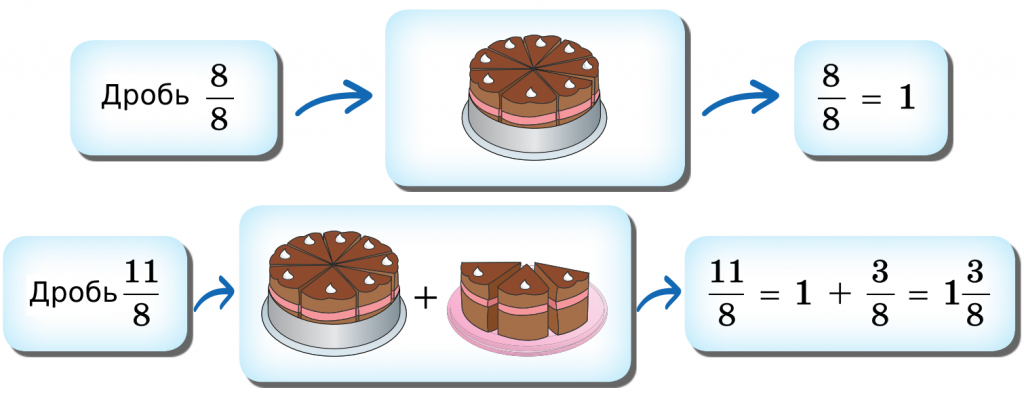
Чтобы превратить смешанное число в неправильную дробь, вы можете просто умножить целое число на знаменатель и добавить числитель, а затем поместить эту сумму над знаменателем.
Например:
2 \frac{3}{4} = (2 x 4) + 3 = 11 => \frac{11}{4} .
С другой стороны, чтобы превратить неправильную дробь в смешанное число, нужно разделить числитель на знаменатель и взять частное как целую часть смешанной дроби, а остаток — как числитель дробной части.
Например:
\frac{11}{4} = 11 : 4 = 2 (целая часть) и 11 — (2 ⋅ 4) = 3 (числитель) => 2 \frac{3}{4}
Важно отметить, что смешанные числа можно использовать в математических действиях, таких как сложение, вычитание, умножение и деление, как и любые другие дроби.
При работе со смешанными числами следует помнить, что их может быть сложнее сравнивать, чем дроби без целой части. При сравнении смешанных дробей вам нужно будет преобразовать их в неправильные дроби с общим знаменателем, прежде чем делать сравнение.
Существуют также другие формы представления смешанных чисел, например, вы можете представить смешанное число в виде десятичной дроби, что является способом выражения числа в виде комбинации целых чисел и десятичных дробей.
Таким образом, смешанные числа являются важным инструментом для выражения и работы с величинами, которые не всегда являются целыми числами. Их можно использовать в математических операциях и измерениях, а также преобразовывать в другие формы представления в зависимости от контекста или задачи.
Обыкновенные дроби 5 класс
