1) Яка з наведених функцій зростає на всій області визначення?
- А) y=x^2
- Б) y=3+\frac{x}{2}
- В) y=\frac{1}{x}
- Г) y=2-3x
2) Знайдіть проміжки спадання функції f(x)=-2x^2+6x-7.
- А) (-\infty; 1,5]
- Б) [1,5; +\infty)
- В) (-\infty; +\infty)
- Г) (-\infty; -1,5]
3) Яке з наведених тверджень неправильне?
- А) Якщо функція f(x) зростає на множині X і a — стала величина, то функція f(x)+a також зростає на цій множині.
- Б) Якщо функція f(x) спадає на множині X і a>0 — стала величина, то функція af(x) також спадає на цій множині.
- В) Якщо функції f(x) і g(x) зростають на множині X, то f(x)+g(x) також зростає на цій множині.
- Г) Якщо функція f(x) не змінює знак на множині X і спадає на цій множині, то \frac{1}{f(x)} також спадає на множині X.
4) Користуючись графіком функції, зображеним на рисунку, вкажіть проміжки зростання цієї функції.
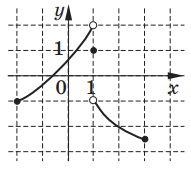
- А) [-2; 1]
- Б) [-1; 2)
- В) (1; 3]
- Г) [-2; 1) і (1; 3]
5) Доведіть, що функція є парною: f(x)=3x^2+x^4.
6) Доведіть, що функція є непарною: f(x)=\frac{3x}{x^6+2}.
7) Дослідіть на парність і непарність функцію: f(x)=|x-2|.
8) Доведіть, що функція f(x) = \frac{1}{x^2} є парною і побудуйте її графік.
