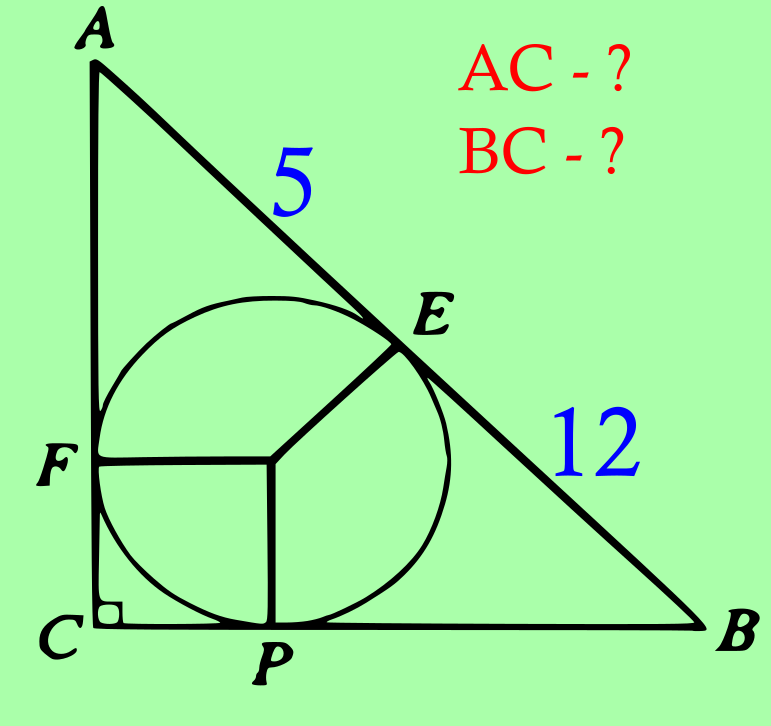
У прямокутному трикутнику точка дотику вписаного кола ділить гіпотенузу на відрізки завдовжки 5 см і 12 см. Знайти катети трикутника.
Розв’язання
За умовою, AE = 5\,\text{см}, BE = 12\,\text{см}. Позначимо через r — радіус вписаного кола.
Маємо:
- BE = BP = 12\,\text{см}
- PC = r
- BC = PC + BP = r + 12
- AE = AF = 5\,\text{см}
- CF = r
- AC = CF + AF = r + 5
- AB = AE + EB = 5 + 12 = 17\,\text{см}
У трикутнику \triangle ABC, кут \angle C = 90^\circ. Згідно з теоремою Піфагора:
AB^2 = AC^2 + BC^2
(r + 12)^2 + (r + 5)^2 = 289
r^2 + 24r + 144 + r^2 + 10r + 25 = 289
2r^2 + 34r + 169 = 289
2r^2 + 34r - 120 = 0
r^2 + 17r - 60 = 0
Розв’язавши квадратне рівняння, отримаємо:
r = 3\,\text{см}
Тоді:
BC = r + 12 = 15\,\text{см}, AC = r + 5 = 8\,\text{см}
Відповідь:
8\,\text{см};\quad 15\,\text{см}
