Самостійна робота 2. Трапеція, Вписані та описані чотирикутники. Оцінювання здійснюється за групами результатів (ГР)
1. Яка рівність повинна виконуватись для сторін чотирикутника ABCD, щоб у нього можна було вписати коло?
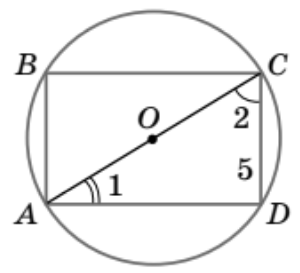
2. ABCD — прямокутник. \angle 2 - \angle 1 = 30^\circ, CD = 5. Знайдіть радіус R описаного кола.
3. Один із кутів рівнобічної трапеції на 120° більший за інший. Учень дійшов висновку, що це сусідні кути, а не протилежні. Чому він правий?
4. Навколо паралелограма описано коло радіуса 5 см. За якою формулою можна обчислити його діагональ d?
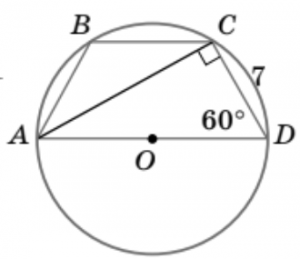
5. ABCD — рівнобічна трапеція, навколо якої описано коло. CD = 7, \angle D = 60^\circ. Знайдіть радіус R цього кола.
6. Чому у довільний прямокутник не завжди можна вписати коло?
7. Прямокутна трапеція з більшою бічною стороною c описана навколо кола з радіусом r. Який вираз представляє периметр P цієї трапеції?
8. ABCD — ромб. \angle ABC : \angle BCD = 1 : 5, радіус вписаного кола r = 3. Знайдіть довжину сторони AB.
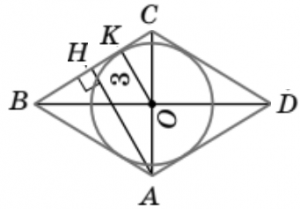
9. Оберіть усі чотирикутники, навколо яких завжди можна описати коло.
10. Установіть відповідність між властивістю чотирикутника (1–3) та умовою, яку ця властивість забезпечує (А–Г).
| 1. | Суми протилежних сторін рівні. |
| 2. | Суми протилежних кутів дорівнюють 180°. |
| 3. | Діагоналі перпендикулярні. |
| А. | Чотирикутник є ромбом. |
| Б. | Можна вписати коло. |
| В. | Можна описати коло. |
| Г. | Чотирикутник є прямокутником. |
| А | Б | В | Г | |
|---|---|---|---|---|
| 1. | ||||
| 2. | ||||
| 3. |
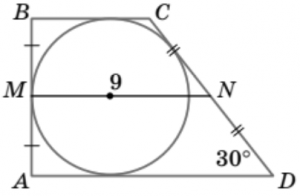
11. ABCD — прямокутна трапеція, в яку вписано коло. Середня лінія MN = 9, \angle D = 30^\circ. Знайдіть довжину більшої бічної сторони CD.
12. Чотирикутник AMNL вписано в коло, і його сторона AM є діаметром. Який висновок можна зробити про кут ANM і чому?
Відповіді до тестових завдань доступні для вчителів з розширеним доступом.

СР2 Трапеція, Вписані чотирикутники 8 клас
