Онлайн тест Середні пропорційні відрізки у прямокутному трикутнику Геометрія 8 клас
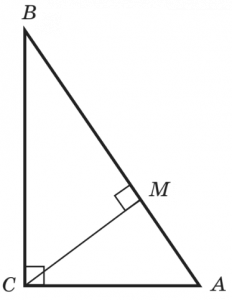
1. У прямокутному трикутнику KML (\angle M = 90^\circ) проведено висоту MN. Укажіть УСІ правильні рівності.
2. Знайдіть висоту прямокутного трикутника, якщо її основа ділить гіпотенузу на відрізки 2 см і 8 см.
3. Знайдіть катет прямокутного трикутника, якщо його проєкція на гіпотенузу і гіпотенуза відповідно дорівнюють 2 см і 18 см.
4. Знайдіть гіпотенузу прямокутного трикутника, якщо один із катетів і його проєкція на гіпотенузу відповідно дорівнюють 10 см і 4 см.
5. Знайдіть висоту прямокутного трикутника, проведену до гіпотенузи, якщо сторони трикутника дорівнюють 9 см, 12 см і 15 см.
6. Установіть відповідність між елементом прямокутного трикутника (1–3) та його довжиною (А–Г).
| 1. | Висота до гіпотенузи, що ділить її на відрізки 4 см і 9 см. |
| 2. | Катет, якщо гіпотенуза 25 см, а проєкція цього катета — 16 см. |
| 3. | Висота до гіпотенузи, якщо катети 15 см і 20 см, а гіпотенуза 25 см. |
| А. | 6 см |
| Б. | 20 см |
| В. | 12 см |
| Г. | 15 см |
| А | Б | В | Г | |
|---|---|---|---|---|
| 1. | ||||
| 2. | ||||
| 3. |
7. Знайдіть середнє пропорційне відрізків завдовжки 25 см і 4 см.
8. Висота, проведена до гіпотенузи, ділить її на відрізки, один з яких 18 см, а другий відноситься до висоти як 1 : 2. Знайдіть висоту трикутника.
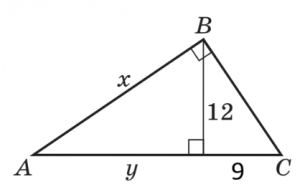
9. Використовуючи властивості прямокутного трикутника з висотою h=12 см та проєкцією одного з катетів на гіпотенузу 9 см, оберіть правильну пару (x; y), де x — довжина катета, що відповідає даній проєкції, а y — довжина іншої проєкції.
10. Перпендикуляр із середини основи рівнобедреного трикутника до бічної сторони ділить її на відрізки 9 см і 7 см, починаючи від вершини. Знайдіть периметр трикутника.
Відповіді до тестових завдань доступне для вчителів з розширеним доступом.
Тест Середні пропорційні відрізки 8 клас
