Самостійна робота 3. Степінь із цілим показником та її властивості

Самостійна робота 3. Степінь із цілим показником та її властивості. Оцінювання здійснюється за групами результатів (ГР)

1. Для будь-яких відмінних від нуля чисел $a$ і $b$ та цілих показників $n$ і $k$ , які з наведених рівностей є правильними? (Оберіть усі правильні варіанти)

a^n \cdot a^k = a^{n+k}

a^n : a^k = a^{n+k}

(a^n)^k = a^{n \cdot k}

(ab)^n = a^n + b^n

{\left(\frac{a}{b}\right)}^{n} = \frac{a^{n}}{b^{n}}

2. Оберіть правильне перетворення, що є ключовим етапом спрощення виразу $b \cdot a^{-n}$ , де $a \neq 0$ і $n$ — натуральне число.

b \cdot a^{-n} = \frac{1}{b \cdot a^n}

b \cdot a^{-n} = \frac{a^n}{b}

b \cdot a^{-n} = \frac{b}{a^n}

b \cdot a^{-n} = \frac{b}{a^{-n}}

3. Які з наведених тверджень щодо степеня з нульовим показником є правильними? (Оберіть усі правильні варіанти)

0^0 = 1

a^0 = 1

для будь-якого дійсного числа

a

a^0 = 1

за умови, що основа

a

відмінна від нуля (

a \neq 0

{\left(\frac{a}{b}\right)}^{0} = 1

за умови, що основи

a

b

відмінні від нуля. Будь-яке від’ємне число у нульовому степені дорівнює -1.

4. Встановіть відповідність між поняттям або виразом (1–3) та ключовим висновком або властивістю (А–Д), що описує його сутність.

Поняття/Вираз
1.	Вираз $a^n \cdot a^{-n}$
2.	Перетворення степеня $a^{-n}$ на дріб
3.	Степінь із цілим показником (як поняття)

Ключовий етап / Висновок
А.	Виконується за формулою $(a^n)^k = a^{n \cdot k}$ .
Б.	$a^0 = 0$ .
В.	Дає результат 1, оскільки $a^n$ та $a^{-n}$ — взаємно обернені числа.
Г.	Об’єднує степінь із натуральним, нульовим та цілим від’ємним показником.
Д.	Виконується за формулою $a^{-n} = \frac{1}{a^n}$ .

	А	Б	В	Г	Д
1.
2.
3.

5. Обчисліть: $4^{-3}$ .

-12

\frac{1}{12}

-64

\frac{1}{64}

6. Установіть відповідність між виразом (1–4) та його значенням (А–Д).

Вираз
1.	$\left(\frac{1}{25}\right)^{-3} : 5^5$
2.	$25^{-5} \cdot 125^3$
3.	$\frac{5^{-9} \cdot (5^3)^{-4}}{5^{-23}}$
4.	$10^{-7} \cdot 5^{10} \cdot 2^7$

Значення
А.	25
Б.	$\frac{1}{5}$
В.	5
Г.	$\frac{1}{25}$
Д.	125

	А	Б	В	Г	Д
1.
2.
3.
4.

7. Спростіть вираз $\left(\frac{2a^{-5}}{a^{-5}-6} + \frac{15a^{-5}}{a^{-10}-12a^{-5}+36}\right) : \frac{2a^{-5}+3}{a^{-10}-36} - \frac{12a^{-5}}{a^{-5}-6}$ . Знайдіть його значення, якщо $a=0,5$ .

8. З-поміж наведених рівностей знайдіть правильні. (Оберіть усі правильні варіанти)

125^{-1} \cdot 25^2 = 5

16^{-3} \cdot 4^6 = 1

(6^2)^6 : 6^{14} = \frac{1}{12}

12^0 : (12^{-1})^2 = 144

\frac{7^{-11}}{7^{-12}} = \frac{1}{7}

9. Сценарій: Учень аналізував рівність $5^{10} \cdot 5^{-11} = -5$ і дійшов висновку, що вона правильна.
Міркування учня:
Крок 1: $5^{10} \cdot 5^{-11} = 5^{10 + (-11)} = 5^{-1}$ .
Крок 2: За правилом перетворення степеня з від’ємним показником $a^{-n} = -a^n$ , отримуємо $5^{-1} = -5^1 = -5$ .
Крок 3: Таким чином, $5^{10} \cdot 5^{-11} = -5$ .
Запитання: На якому кроці в обґрунтуванні учня допущено помилку?

Крок 1 (Помилка при додаванні показників) Крок 2 (Неправильне застосування правила перетворення степеня

5^{-1}

) Крок 3 (Неправильний висновок) Помилки немає, усі кроки правильні

10. Сценарій: Учень розкладав на множники вираз $a^{-4} + 2a^{-2}b^{-4} + b^{-8}$ .
Розв’язок:
Крок 1: $a^{-4} + 2a^{-2}b^{-4} + b^{-8} = \frac{1}{a^4} + \frac{2}{a^2b^4} + \frac{1}{b^8}$ .
Крок 2: $(\frac{1}{a^2})^2 + 2 \cdot (\frac{1}{a^2}) \cdot (\frac{1}{b^4}) + (\frac{1}{b^4})^2$ .
Крок 3: Застосування формули: $\left(\frac{1}{a^2} + \frac{1}{b^4}\right)^2$ .
Крок 4: Повернення до від’ємних степенів: $(a^2 + b^4)^{-2}$ .
Запитання: У якому кроці учень припустився помилки в логіці розкладання або в перетворенні степенів?

Крок 1 (Неправильне перетворення виразу

2a^{-2}b^{-4}

) Крок 2 (Неправильне виділення елементів для формули квадрата) Крок 3 (Помилка при застосуванні формули квадрата суми) Крок 4 (Неправильне перетворення суми степенів

\left(\frac{1}{a^2} + \frac{1}{b^4}\right)

назад у від’ємний степінь)

11. Сценарій: Функцію задано виразом: $y = \frac{2x^{-2} - 4x^{-1}}{x^{-3} - 2x^{-2}} - \frac{4x^{-3} - 4x^{-2}}{x^{-4} - x^{-3}}$ . Після скорочення функція зводиться до $y = -2x$ . Учень побудував графік прямої $y=-2x$ (без виключення точок) і стверджує, що оскільки $y=-2x$ — це пряма, то його графік є правильним.
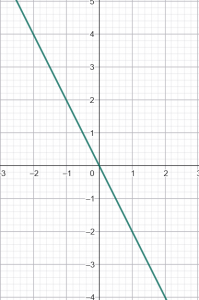Запитання: Графік, побудований учнем, є помилковим. Які з наведених тверджень правильно пояснюють його помилку та вказують на необхідні виправлення?

Учень не врахував, що при спрощенні функція

y = -2x

має проходити через початок координат. Учень не визначив Область Допустимих Значень (ОДЗ) і не виключив з графіка точки, де знаменники початкового дробу дорівнюють нулю. Треба виключити дві виколоті точки ОДЗ:

x=0

та

x=1

. Треба виключити дві виколоті точки ОДЗ:

x=0

та

x=-1

. Треба виключити три виколоті точки ОДЗ:

x=0

x=\frac{1}{2}

x=1

12. Установіть відповідність між хибним перетворенням (1–3) та типом помилки (А–Д).

Хибне перетворення
1.	$25 - a^{-4} = (5 - a^{-2})(5 + a^{-2})$
2.	$\frac{1}{(a-b)^2} = a^{-2} - b^{-2}$
3.	$\left(\frac{a}{b}\right)^{-2} = \frac{a^2}{b^{-2}}$

Тип помилки
А.	Помилка властивості: Неправильно застосовано правило $(\frac{a}{b})^n = \frac{a^n}{b^n}$ .
Б.	Помилка формули: Ігнорування дужок при розкладанні різниці квадратів.
В.	Помилка означення: Неправильна інтерпретація від’ємного степеня; вираз $a^{-n}$ не може бути від’ємним числом.
Г.	Помилка формули: Неправильне застосування формули скороченого множення до суми/різниці виразів у знаменнику.
Д.	Помилка властивості: Неправильне застосування правила $\left(\frac{a}{b}\right)^{-n} = \left(\frac{b}{a}\right)^n$ .

	А	Б	В	Г	Д
1.
2.
3.

Відповіді до тестових завдань доступні для вчителів з розширеним доступом.

СР3 Степінь із цілим показником та її властивості 8 клас