Вертикальні кути. Кут між двома прямими, що перетинаються
Завантажити презентацію Вертикальні кути 7 клас НУШ
Зображення слайду | Текстове пояснення |
 | Титульний слайд Вертикальні кути. Кут між двома прямими, що перетинаються |
 | Якщо люди не сміються над твоїми цілями, твої цілі занадто маленькі |
| Сьогодні на уроці: Які кути називаються вертикальними? Як побудувати кут, вертикальний до даного кута? Теорема про вертикальні кути. | |
 | Які промені називають доповняльними? Що таке аксіома, теорема, означення? Які кути називають суміжними? Чому дорівнює сума суміжних кутів? |
 | Ножиці знайомі всім. Скільки всяких цікавих речей ви ними вирізали… Але чи замислювалися ви, чому, коли наближати кільця одне до одного, одночасно одне до одного наблизяться кінці з лезами? |
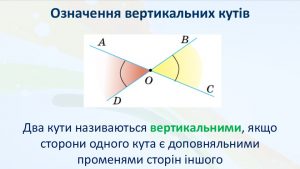 | Означення вертикальних кутів Два кути називаються вертикальними, якщо сторони одного кута є доповняльними променями сторін іншого |
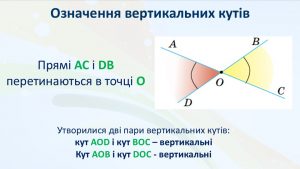 | Прямі АС і DB перетинаються в точці О Утворилися дві пари вертикальних кутів: кут AOD і кут BOC – вертикальні Кут AOB і кут DOC – вертикальні |
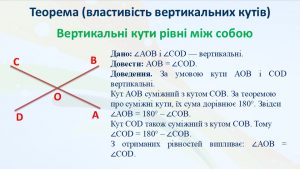 | Теорема (властивість вертикальних кутів) Вертикальні кути рівні між собою Дано: ∠АОВ і ∠СОD — вертикальні. Довести: АОВ = ∠СОD. Доведення. За умовою кути АОВ і СОD вертикальні. Кут АОВ суміжний з кутом СОВ. За теоремою про суміжні кути, їх сума дорівнює 180°. Звідси ∠АОВ = 180° – ∠СОВ. Кут CОD також суміжний з кутом СОВ. Тому ∠CОD = 180° – ∠СОВ. З отриманих рівностей випливає: ∠АОВ = ∠СОD. |
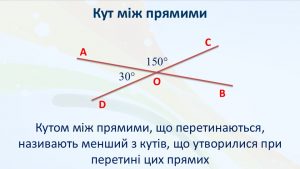 | Кут між прямими Кутом між прямими, що перетинаються, називають менший з кутів, що утворилися при перетині цих прямих |
 | Задача 1. Сума вертикальних кутів дорівнює 110°. Яка градусна міра цих кутів? |
 | Розв’язок |
 | Задача 2. Прямі а і b перетинаються під кутом 30°. Знайдіть градусну міру трьох інших кутів. |
 | Розв’язок |
 | Задача 3. Сума двох кутів, що утворилися в результаті перетину двох прямих, дорівнює 100°. Знайдіть усі утворені кути. |
 | Розв’язок |
 | Задача 4. Знайди міри кутів, утворених при перетині двох прямих, якщо один із них на 20° менший за інший. |
 | Розв’язок |
 | Задача 5. На рисунку ∠ ABE = ∠ DCP. Доведіть, що ∠ FBC + ∠BCP = 180°. |
 | Розв’язок |
 | Задача 6. Два із чотирьох нерозгорнутих кутів, що утворилися при перетині двох прямих, відносяться як 4 : 5. Знайти градусну міру кожного з кутів, що утворилися. |
 | Розв’язок |
 | Експрес-контроль 1 |
 | ПРИГАДАЙТЕ ГОЛОВНЕ Які кути називають вертикальними? Яку властивість мають вертикальні кути? Який кут називають кутом між двома прямими? |
 | Підсумок уроку |
 | Матеріали для презентації Підручник Геометрія 7 клас (О. Істер) Підручник Геометрія 6 клас (М. Бурда, Н. Тарасенкова) Підручник Геометрія 7 клас (А. Єршова) Підручник Геометрія 7 клас (Г. Бевз) Підручник Геометрія 7 клас (А. Мерзляк) |
