Самостійна робота призначена для учнів 7 класу за програмою НУШ на тему “Зв’язки між величинами. Функція. Способи задання функції”. Пропонується розв’язати 6 завдань різного рівня складності та 4 варіанти. Ця самостійна робота допоможе учням та вчителю перевірити знання теми. Автор М. Якир – від Мерзляків
Варіант 1
1. Функцію задано формулою \mathit{f}(x) = x^2 - 4 . Укажіть неправильну рівність.
2. На рисунку зображено графік залежності частоти пульсу гімнаста (кількість ударів серця на хвилину) від часу протягом та після його виступу у вільних вправах. Визначте, користуючись графіком, частоту пульсу через 1 хв після початку виступу.
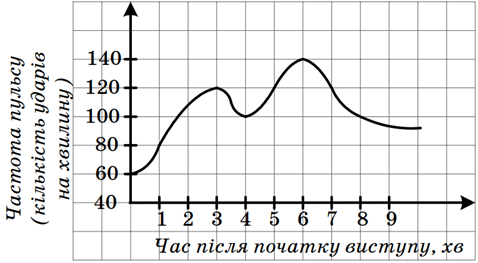
3. Користуючись графіком, зображеним на рисунку, визначте:
1) частоту пульсу гімнаста перед початком виступу;
2) якою була найбільша частота пульсу та через скільки хвилин після початку виступу;
3) через скільки хвилин після початку виступу частота пульсу становила 120 ударів на хвилину.
4. Кожному натуральному числу, яке більше за 10, але менше від 20, поставили у відповідність остачу при діленні цього числа на 4. Задайте цю функцію таблично.
5. Дано функцію f(x) = \begin{cases} x^3, & \text{якщо } x \leq 1, \\2x - 1, & \text{якщо } x > 1. \end{cases}
Знайдіть:
1) \mathit{f}(-2); 2) \mathit{f}(0); 3) \mathit{f}(1); 4) \mathit{f}(6).
6. Функції задано формулами y= x^2 - 5x і y = x - 9. При якому значенні аргументу ці функції набувають рівних значень?
Варіант 2
1. Функцію задано формулою \mathit{f}(x) = x^2 + 4 . Укажіть неправильну рівність.
2. На рисунку зображено графік зміни температури розчину протягом хімічного досліду. Визначте, користуючись графіком, температуру розчину через 10 хв після початку досліду.
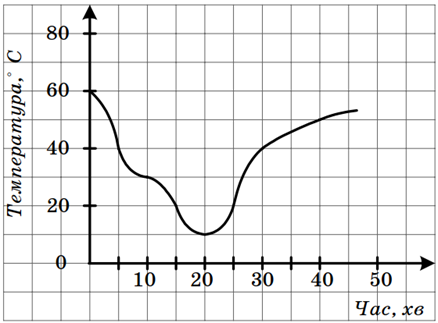
3. Користуючись графіком, зображеним на рисунку, визначте:
1) якою була початкова температура розчину;
2) якою була найнижча температура розчину та через скільки хвилин після початку досліду;
3) через скільки хвилин після початку досліду температура розчину дорівнювала 40°С.
4. Кожному натуральному числу, яке більше за 20, але менше від 30, поставили у відповідність остачу при діленні цього числа на 7. Задайте цю функцію таблично.
5. Дано функцію f(x) = \begin{cases} 3x + 2, & \text{якщо } x \leq 2, \\x^3, & \text{якщо } x > 2. \end{cases}
Знайдіть:
1) \mathit{f}(-1); 2) \mathit{f}(0); 3) \mathit{f}(2); 4) \mathit{f}(3).
6. Функції задано формулами y= x^2 + 3x і y = -x - 4. При якому значенні аргументу ці функції набувають рівних значень?
Варіант 3
1. Функцію задано формулою \mathit{f}(x) = x^2 - 4x . Укажіть неправильну рівність.
2. На рисунку зображено графік залежності швидкості автомобіля від часу протягом перших 3 хв після початку руху. Визначте, користуючись графіком, швидкість автомобіля через 20 с після початку руху.
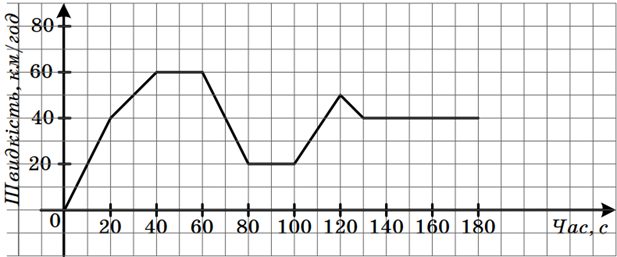
3. Користуючись графіком, зображеним на рисунку, визначте:
1) якою була найбільша швидкість автомобіля та протягом якого часу;
2) через скільки секунд після початку руху швидкість автомобіля складала 50 км/год;
3) протягом якого проміжку часу швидкість автомобіля зменшилася зі 60 км/год до 20 км/год.
4. Кожному натуральному числу, яке більше за 30, але менше від 40, поставили у відповідність остачу при діленні цього числа на 6. Задайте цю функцію таблично.
5. Дано функцію f(x) = \begin{cases} 6, & \text{якщо } x \leq -2, \\ x + 1, & \text{якщо } -2 < x < 0, \\ 1 - 3x, & \text{якщо } x >= 0. \end{cases}
Знайдіть:
1) \mathit{f}(-3); 2) \mathit{f}(-2); 3) \mathit{f}(-1,6); 4) \mathit{f}(4).
6. Функції задано формулами y= x^3 - x + 1 і y = 8x + 1. При яких значеннях аргументу ці функції набувають рівних значень?
Варіант 4
1. Функцію задано формулою \mathit{f}(x) = x^2 + 4x . Укажіть неправильну рівність.
2. Рейсовий автобус пройшов увесь маршрут за 20 хв. На дорозі між кінцевими зупинками відсутні світлофори. На рисунку зображено графік залежності швидкості автобуса від часу. Визначте, користуючись графіком, швидкість автобуса через 5 хв після початку руху.
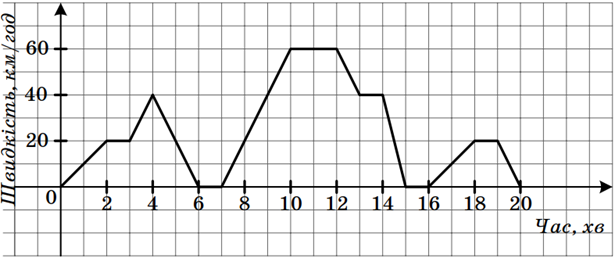
3. Користуючись графіком, зображеним на рисунку, визначте:
1) якою була найбільша швидкість автобуса та протягом якого часу;
2) скільки зупинок зробив автобус протягом усього маршруту та якою є тривалість кожної з них;
3) за скільки хвилин після другої зупинки швидкість автобуса зросла до 20 км/год.
4. Кожному натуральному числу, яке більше за 40, але менше від 50, поставили у відповідність остачу при діленні цього числа на 5. Задайте цю функцію таблично.
5. Дано функцію f(x) = \begin{cases} x + 2, & \text{якщо } x \leq -1, \\-4 - 5x, & \text{якщо } -1 < x < 0, \\7, & \text{якщо } x >= 0. \end{cases}
Знайдіть:
1) \mathit{f}(-2.3); 2) \mathit{f}(-1); 3) \mathit{f}(0); 4) \mathit{f}(2).
6. Функції задано формулами y= 4x - 5 і y = x^3 - 12x - 5. При яких значеннях аргументу ці функції набувають рівних значень?
Завантажити Самостійну роботу Зв’язки між величинами. Функція. Способи задання функції для друку
